An Introduction to measuring risk in the TSP Funds

[Cactus]

Part 1
​

We hear a lot about investment risk but what exactly is it? Yes, I know it involves losing your shirt and eating Alpo in retirement, but let's forget about emotions here and talk about the numbers. How do you measure risk and more importantly what do you do with it? These are questions I've had that are hard to answer, so I thought I would give it a try -- a start of one any ways.

When talking about risk, we here terms thrown around like Risk On, Risk Off, Alpha, Beta, r-squared, Volatility, etc. It's enough to make my head spin. Volatility is a popular measure of risk we here a lot today. As it turns out, this is something we can measure by calculating something called a Standard Deviation. Now there's a term I finally recognize. It's something I remember from plotting lines to data points on a graph in school. Since this is something I can understand, that is what I'll talk about in this article.

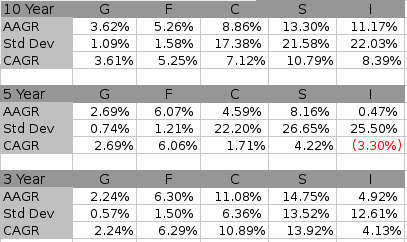
A Standard Deviation is a statistical term that measures how much individual values differ from their mean or average value. Huh??? Maybe this will be easier to understand with an example. I direct you're attention to table 1 below.

[TD="align: left"] Table 1 [/TD]
[TD="bgcolor: #969696, align: left"]Period 1[/TD]
[TD="bgcolor: #969696, align: left"]Period 2[/TD]
[TD="bgcolor: #969696, align: left"]Period 3[/TD]
[TD="bgcolor: #969696, align: left"]Period 4[/TD]
[TD="bgcolor: #969696, align: left"]Period 5[/TD]
[TD="bgcolor: #969696, align: left"]Period 6[/TD]
[TD="bgcolor: #969696, align: left"]AAGR[/TD]
[TD="bgcolor: #969696, align: left"]Std Dev[/TD]
[TD="bgcolor: #969696, align: left"]CAGR[/TD]

[TD="bgcolor: #C0C0C0, align: left"]Example 1[/TD]
[TD="align: right"]6.00%[/TD]
[TD="align: right"]6.00%[/TD]
[TD="align: right"]6.00%[/TD]
[TD="align: right"]6.00%[/TD]
[TD="align: right"]6.00%[/TD]
[TD="align: right"]6.00%[/TD]
[TD="align: right"]6.00%[/TD]
[TD="align: right"]0.00%[/TD]
[TD="align: right"]6.00%[/TD]

[TD="bgcolor: #C0C0C0, align: left"]Example 2[/TD]
[TD="align: right"]5.00%[/TD]
[TD="align: right"]7.00%[/TD]
[TD="align: right"]5.00%[/TD]
[TD="align: right"]7.00%[/TD]
[TD="align: right"]5.00%[/TD]
[TD="align: right"]7.00%[/TD]
[TD="align: right"]6.00%[/TD]
[TD="align: right"]1.00%[/TD]
[TD="align: right"]6.00%[/TD]

[TD="bgcolor: #C0C0C0, align: left"]Example 3[/TD]
[TD="align: right"]12.00%[/TD]
[TD="align: right"]0.00%[/TD]
[TD="align: right"]12.00%[/TD]
[TD="align: right"]0.00%[/TD]
[TD="align: right"]12.00%[/TD]
[TD="align: right"]0.00%[/TD]
[TD="align: right"]6.00%[/TD]
[TD="align: right"]6.00%[/TD]
[TD="align: right"]5.83%[/TD]

[TD="bgcolor: #C0C0C0, align: left"]Example 4[/TD]
[TD="align: right"]18.00%[/TD]
[TD="align: right"]−6.00%[/TD]
[TD="align: right"]18.00%[/TD]
[TD="align: right"]−6.00%[/TD]
[TD="align: right"]18.00%[/TD]
[TD="align: right"]−6.00%[/TD]
[TD="align: right"]6.00%[/TD]
[TD="align: right"]12.00%[/TD]
[TD="align: right"]5.32%[/TD]

When I first started working for the government, we were encouraged to buy EE Bonds which payed a rate based on the 10-year Treasury but had a guaranteed minimum of 6%. Since the Treasury rate was already below this, we kept getting 6% every period. I show this over 6 periods in row 1 (Example 1) of table 1. That means my average return is 6% and the Stardard Deviation is 0. Why 0? Because none of the periods deviates from the average value. They are all 6%.

OK, let's stir things up by introducing some volatility as shown in examples 2 - 4. Each row shows periods with progressively larger deviations from the mean (average value). The average, which is in the column labeled AAGR (Average Annual Growth Rate), is still 6% but the Standard Deviation (Std Dev) increases with the period volatility for each successive row.

If you look at the examples I've given you, you will notice that each period is exactly above or below the average by the value of the Std Dev. It's not like that in the real world. This only happened here because of the regular pattern of the data I chose to show you how the Std Dev increases with volatility. With real world data that follows a Gaussian distribution, only 68.27% of the data will be within 1 Std Dev of the mean. 95.45% will be within 2 Std Dev and 99.73% will be within 3. I won't go into why or what all that means but instead I'll direct you here for further reading if you are interested.

What I want to do here is show you how to calculate these values with a spreadsheet like Excel so you can calculate your own Std Dev from your data and see how they compare to each other and the mean. If you type the data of table 1 into a spreadsheet starting in cell A1 and proceeding through G5, you can easily calculate the values of AAGR & Std Dev in columns H & I by using built-in functions of the spreadsheet.

AAGR is simply the mean or average we are all familiar with. As the name suggests it is dealing with annual returns, but you can calculate a mean and Std Dev of any period. In fact, when we here about volatility picking up they are usually referring to daily or intraday values.

To calculate the mean you could simply add the 6 entries in each row and divide by 6, but we are going to use the "AVERAGE" function here to make it easier. To compute the AAGR of Example 1 type the following into cell H2:

= AVERAGE(B2:G2)

What this cell entry is saying is: take all values between B2 & G2 inclusive and return the average. It should come out to 6% or 0.06 depending on how you have the cell formated. Note that you could have selected that range with your mouse after typing '= AVERAGE(' and it would have filled it in for you. Just hit the enter key after that and you're done. You can do the same thing for the other rows but why? Just click your mouse in H2, select the little square in the lower right hand corner of the cell and drag it down the column to fill those entries auto-adjusting the cell references as it goes. There you are. You have your averages in column H.

OK, now we do the same thing for the Std Dev in column I. If you want to know how to do this manually, check out the reference I gave you earlier. We are going to use the built in function for the population standard deviation (also called N standard deviation) here. Here is where you are going to have to see what it is actually called in your spreadsheet. Common names are STDEV.P or STDEVP. You should be able to start typing it and the spreadsheet will give you options and descriptions from its library. Once you find it type it in like so:

= STDEV.P(B2:G2)

That should be all there is to it. Note that if you are getting results larger than what I show, you may be using a sample standard deviation (also called N-1 standard deviation) by mistake. It is often called STDEV.S, STDEVS, or simply STDEV. That one is for taking random samples from a population instead of a continuous series for a period of time like we are doing here.

OK, that's probably all that will fit in this entry, so I will conclude this as part 1 and continue in part 2. As for now you should be able to take your own data and compute your own standard deviations to compare the volatility of one data set to the next. Have fun.

 

[Cactus]

Part 2
​

In part 1 we computed the AAGR & Std Dev of a series of fictitious returns to show that the Std Dev goes up with the volatility while the AAGR or mean average remains the same. Big deal! If I'm getting 6% it's 6%; what do I care about the Std Dev. Well, it's only 6% over the so called long run and you incur the risk of actually earning 6% +/- the Std Dev in any one period. The larger the Std Dev the more you could earn or lose, and it's the lose we are concerned about here.

Now for the real kicker. You aren't really earning 6%. You see, there's more than one type of average and you aren't earning the AAGR. You probably guessed that by now from puzzling over that last column of table 1 labeled CAGR where the percentages actually decrease with increasing Std Dev. Yep, that's the average you're getting. That is the Compound Annual Growth Rate and it is the equivalent return you would have earned if you earned the same amount in each period. By the way, that is why the AAGR is the same as the CAGR for Example 1. Now your head is spinning, but it's not really that hard. In fact you knew this intuitively all along. I'll show you with a common example.

It's the end of 2008. You started the year with let's say $100 in your TSP account but after losing 50% you are down to $50. You pull your money out of the market for the 1st quarter of 2009 while you drown your sorrows, but as you sober up you discover that you timed your trades just right for the rest of 2009 and you earned 50%. Sounds great! You made up your losses from the previous year, right? -50% + 50% averages to 0%. That is the AAGR, so why do you only have $75 in your TSP account. It's because the 50% gain is on a smaller amount, not the original amount you started with and lost. That is why losses hurt more than gains help. That is why a large negative Std Dev is not made up for by an equivalently large positive Std Dev. Turning the loss/gain around to a gain/loss doesn't help you either. In that case even though your initial gain is on the original amount, your subsequent loss is now on the newer larger amount. You lose the same amount either way. You know this. You've been there just like me. So let's compute what we really got, shall we? The formula for the CAGR is relatively simple and is given by:

CAGR = [(FV/PV)^(1/number of periods)] - 1

What? You don't thinks that's all that simple. How about we use another built-in function instead. We can use the RRI function which has the following syntax:

 = RRI(NPER, PV, FV)

If your spreadsheet doesn't have the RRI function, you can substitute the RATE function in its place. It has the following syntax:

 = RATE(NPER, PMT, PV, FV)

The RATE function is set up to calculate the interest rate on paying off a debt (PV) down to (FV) amount in (NPER) equal payments of (PMT). In our case we don't hold a debt but own the principle so we have to negate the value of PV. We also won't be making any payments or withdrawing any principle so our PMT is 0. Plugging in 2 years for NPER and $75 for FV gives us:

CAGR = RATE(2,0,-100,75) = RRI(2,100,75) = [COLOR=#ff0000]-13.4%[/COLOR]

Now that looks like what happened to us! Going from $100 to $75 in two years is like losing 13.4% a year. That makes a lot more sense than breaking even at 0%.

We can use this function to compute the CAGR in table 1 but things are a bit more complex because we don't have PVs and FVs but a series of gains and losses. It turns out we can use another function, "FVSCHEDULE", to generate a FV for a dummy PV, of say 1. Plugging that into the RRI or RATE equation in cell J2 gives us:

= RRI(COUNT(B2:G2), 1, FVSCHEDULE(1, B2:G2))

or

= RATE(COUNT(B2:G2), 0, -1, FVSCHEDULE(1, B2:G2))

Drag this entry down the column as before and you should see the values in the last column of table 1. Note that instead of just entering a 6 for the count I used another built-in function to compute that. That may seam like an unnecessary complexity in a simple example like this, but with real world data sets it helps prevent change errors. If I change the range B2:G2 in any way I need to change the 6 to the new value. That is too easy to forget or even to miscount. Setting it up with a function like this I only need to make sure the ranges for COUNT match the ranges for FVSCHEDULE.

As an aside, the function FVSCHEDULE is what we typically use to calculate our total return over all periods. You could add column K to your spreadsheet to show the total return over 6 period by typing the following into cell K2:

= FVSCHEDULE(1, B2:G2) - 1

You Should get something like this in column K.

[TD="align: left"] Table2 [/TD]

[TD="bgcolor: #969696, colspan: 2, align: left"]Total Return[/TD]

[TD="align: right"]41.85%[/TD]

[TD="align: right"]41.81%[/TD]

[TD="align: right"]40.49%[/TD]

[TD="align: right"]36.47%[/TD]

[TD="align: right"]41.74%[/TD]

This looks like a good place to stop for now. In part three of the article we'll used what we learned here on the annual returns of our TSP funds and see what that tells us. Stay tuned.

 

[Cactus]

Part 3
​

In parts 1 & 2 of this article we talked about averages and risk as measured by standard deviations. We showed how to calculate these values and included some dummy examples to clarify the point.

OK, enough with examples already. It's time to try some real data. This is supposed to be measuring risk in the TSP Funds so let's do that. I grabbed the annual returns of our 5 funds back to the inception of the latest additions (S & I Fund) and posted them in table 3 below:

Table 3

[TD="bgcolor: #969696, align: left"]Year[/TD]
[TD="bgcolor: #969696, align: center"]G[/TD]
[TD="bgcolor: #969696, align: center"]F[/TD]
[TD="bgcolor: #969696, align: center"]C[/TD]
[TD="bgcolor: #969696, align: center"]S[/TD]
[TD="bgcolor: #969696, align: center"]I[/TD]

[TD="bgcolor: #C0C0C0, align: right"]2001[/TD]
[TD="align: right"]5.39%[/TD]
[TD="align: right"]8.61%[/TD]
[TD="align: right"] (11.94%)
[/TD]
[TD="align: right"] (9.04%) [/TD]
[TD="align: right"] (21.94%) [/TD]

[TD="bgcolor: #C0C0C0, align: right"]2002[/TD]
[TD="align: right"]5.00%[/TD]
[TD="align: right"]10.27%[/TD]
[TD="align: right"] (22.05%) [/TD]
[TD="align: right"] (18.14%) [/TD]
[TD="align: right"] (15.98%) [/TD]

[TD="bgcolor: #C0C0C0, align: right"]2003[/TD]
[TD="align: right"]4.11%[/TD]
[TD="align: right"]4.11%[/TD]
[TD="align: right"]28.54%[/TD]
[TD="align: right"]42.92%[/TD]
[TD="align: right"]37.94%[/TD]

[TD="bgcolor: #C0C0C0, align: right"]2004[/TD]
[TD="align: right"]4.30%[/TD]
[TD="align: right"]4.30%[/TD]
[TD="align: right"]10.82%[/TD]
[TD="align: right"]18.03%[/TD]
[TD="align: right"]20.00%[/TD]

[TD="bgcolor: #C0C0C0, align: right"]2005[/TD]
[TD="align: right"]4.49%[/TD]
[TD="align: right"]2.40%[/TD]
[TD="align: right"]4.96%[/TD]
[TD="align: right"]10.45%[/TD]
[TD="align: right"]13.63%[/TD]

[TD="bgcolor: #C0C0C0, align: right"]2006[/TD]
[TD="align: right"]4.93%[/TD]
[TD="align: right"]4.40%[/TD]
[TD="align: right"]15.79%[/TD]
[TD="align: right"]15.30%[/TD]
[TD="align: right"]26.32%[/TD]

[TD="bgcolor: #C0C0C0, align: right"]2007[/TD]
[TD="align: right"]4.87%[/TD]
[TD="align: right"]7.09%[/TD]
[TD="align: right"]5.54%[/TD]
[TD="align: right"]5.49%[/TD]
[TD="align: right"]11.43%[/TD]

[TD="bgcolor: #C0C0C0, align: right"]2008[/TD]
[TD="align: right"]3.75%[/TD]
[TD="align: right"]5.45%[/TD]
[TD="align: right"] (36.99%)
[/TD]
[TD="align: right"] (38.32%) [/TD]
[TD="align: right"] (42.43%) [/TD]

[TD="bgcolor: #C0C0C0, align: right"]2009[/TD]
[TD="align: right"]2.97%[/TD]
[TD="align: right"]5.99%[/TD]
[TD="align: right"]26.68%[/TD]
[TD="align: right"]34.85%[/TD]
[TD="align: right"]30.04%[/TD]

[TD="bgcolor: #C0C0C0, align: right"]2010[/TD]
[TD="align: right"]2.81%[/TD]
[TD="align: right"]6.71%[/TD]
[TD="align: right"]15.06%[/TD]
[TD="align: right"]29.06%[/TD]
[TD="align: right"]7.94%[/TD]

[TD="bgcolor: #C0C0C0, align: right"]2011[/TD]
[TD="align: right"]2.45%[/TD]
[TD="align: right"]7.89%[/TD]
[TD="align: right"]2.11%[/TD]
[TD="align: right"](3.38%)[/TD]
[TD="align: right"](11.81%)[/TD]

[TD="bgcolor: #C0C0C0, align: right"]2012[/TD]
[TD="align: right"]1.47%[/TD]
[TD="align: right"]4.29%[/TD]
[TD="align: right"]16.07%[/TD]
[TD="align: right"]18.57%[/TD]
[TD="align: right"]18.62%
[/TD]

[TD="bgcolor: #C0C0C0, align: left"]AAGR[/TD]
[TD="align: right"]3.88%
[/TD]
[TD="align: right"]5.96%[/TD]
[TD="align: right"]4.55%[/TD]
[TD="align: right"]8.82%[/TD]
[TD="align: right"]6.15%[/TD]

[TD="bgcolor: #C0C0C0, align: left"]Std Dev[/TD]
[TD="align: right"]1.16%[/TD]
[TD="align: right"]2.15%[/TD]
[TD="align: right"]18.68%[/TD]
[TD="align: right"]22.18%[/TD]
[TD="align: right"]23.06%
[/TD]

[TD="bgcolor: #C0C0C0, align: left"]CAGR[/TD]
[TD="align: right"]3.87%[/TD]
[TD="align: right"]5.94%[/TD]
[TD="align: right"]2.63%[/TD]
[TD="align: right"]6.27%[/TD]
[TD="align: right"]3.25%[/TD]

[TD="bgcolor: #C0C0C0, align: left"]Total[/TD]
[TD="align: right"]57.75%[/TD]
[TD="align: right"]99.80%[/TD]
[TD="align: right"]36.52%[/TD]
[TD="align: right"]107.51%[/TD]
[TD="align: right"]46.79%[/TD]

There you have it, our TSP funds for the last 12 years. What can we make of this? To start with we see a lot that we already know or think we know. The risk (Std Dev) is much larger for the equity funds (C,S, & I) than it is for the G & F funds. That is to be expected for something that has the potential for greater gains. Unfortunately this span of time covers most of 2 periods of economic decline, termed a secular bear market, that produced less than stellar returns. Comparing the CAGR of the equity funds to those of G & F shows no clear advantage. Comparing each fund's return to its Std Dev makes the equity funds look like they aren't even worth the risk. The risk in G & F is less than half the return while for equities they are several multiples larger. If we had seen these numbers before, we would not have invested in equities. The F Fund was obviously the way to go, producing greater total returns over this period than the C & I Funds combined.

So does this mean we should abandon equities? Only if you expect this pattern to continue and recently it hasn't. Don't you wish you'd been in the S or C Fund for all of 2013 so far? Not to mention last year? You have to remember we are looking at 12 years of recent data that was largely effected by 2 declines. Does this have an overly negative impact on our numbers? The numbers do change with the time span included. Try running the numbers on the last 10, 5, & 3 years and you should get the results shown in table 4 below. Interestingly enough, the CAGR changes quite a bit for the equity funds while the Std Dev stays around the same ball park values. That is until we get down to 3 years where we effectively cut out both economic declines. Not a good idea. A better idea is to increase our time span. You can go back to the late 80s if you cut out the S & I Funds. Check out Table 5. Again you will find that the Std Dev of the C Fund is within the same ball park figure but the average returns are greater because of the booming 90s.

Table 4: 10, 5, & 3 year returns


Table 5: 1988 - 2012

[TD="bgcolor: #969696, align: left"]1988 - 2012[/TD]
[TD="bgcolor: #969696, align: center"]G[/TD]
[TD="bgcolor: #969696, align: center"]F[/TD]
[TD="bgcolor: #969696, align: center"]C[/TD]

[TD="bgcolor: #C0C0C0, align: left"]AAGR[/TD]
[TD="align: right"]5.62%[/TD]
[TD="align: right"]7.11%[/TD]
[TD="align: right"]11.12%[/TD]

[TD="bgcolor: #C0C0C0, align: left"]Std Dev[/TD]
[TD="align: right"]2.01%[/TD]
[TD="align: right"]4.66%[/TD]
[TD="align: right"]17.80%[/TD]

[TD="bgcolor: #C0C0C0, align: left"]CAGR[/TD]
[TD="align: right"]5.60%[/TD]
[TD="align: right"]7.00%[/TD]
[TD="align: right"]9.50%[/TD]

Given all that, it looks like it's fair to conclude that our values for risk are fairly consistent for equities so we can use those values from table 3 even if the average returns are lower than historical norms. The 2 declines don't appear to have skewed the Std Dev since table 3's 12 years, table 4's 10 years and table 5's 24 years are all close for the C Fund. If anything, the most recent decline by itself had more of a negative impact in that the table 4's 5 year Std Dev is higher than the previous 3 mentioned.

You want to look at even more historical data? Another option is to use the actual data from the markets our funds are indexed too. For example our C Fund is indexed to the S&P 500 so you can use that from a site like this one to calculate the AARG, Std Dev, and CAGR. That site will let you compute those right on the web page all the way back to the 1870s if you want to.

The thing to keep in mind is to be consistent. What you want to do is get an idea of your potential gain verses the risk it could cost you. Looking at table 3 shows you still made the most in the S Fund, but with a Std Dev almost 4 times the return was it worth it? That's a question only you can answer, but I'm sure you would have been more comfortable earning slightly less in the F Fund with a risk less than half the return. That's the kind of risk analysis and comparisons I'm looking at anyways. And if you don't want to keep all your eggs in one basket that's even better. You can spread your risk out over several funds like the L Funds do in order to get the desired return with less risk. Choosing a 50:50 allocation of F & S from table 3, for example, would give you an equivalent CAGR of 6.10% with a Std Dev of 12.16%. It's all up to you. I only give you the numbers to show you how to be careful.

 

[nnuut]

Please post a link to your source.

 

[Cactus]

Part 4
​

OK, are there any surprises. Well, I was surprised the F Fund returned that much. I always thought of the F Fund as not returning very much but doing better than the G Fund when equities are down. Looking at table 3 we see that it doesn't have the large gains like the equity funds but it also doesn't have any loses. As we've seen before, the lack or reduction of losses really helps you. It's what you want. The F Fund has had negative years, of course. It was down in 1994, 1999, and so far this year 2013, but that is far fewer than what we have with equities. One other thing to note, though, are the significant differences in the Std Dev between tables 3 & 5. When you go back to 1988 the Std Dev more than doubles what it is in the last 12 years even though the average returns aren't vastly different. That is something you may want to take into account.

The other thing that is surprising is that the G Fund has any risk at all. What's up with that? I thought the G Fund is where you parked your money so you won't lose it. How can it have risk? Well, you have to remember what we are measuring here: the deviation from the mean. The reason the G Fund has a non-zero Std Dev is because its returns are not constant but have been decreasing over the range included. We tend to think of risk as loosing money but what is actually being measured here is the likelihood of being greater or smaller than the average. Now most people have no problem with being over the average. It's being below that bothers us. But in the case of the G Fund, above or below, we are still earning something and even if we don't we aren't loosing our money. The G Fund these days is all about the preservation of capital, not about making money. Maybe we shouldn't use Std Dev for the G Fund and just assign it a value of 0. I don't know. I don't expect to earn the average of a 12 year range. I expect to get tomorrow what I got yesterday. You could plot a line through the data points using linear regression and measure the Std Dev to the line instead of the mean to get a much smaller value, but I don't think it's worth it. Just use it as is or set it to 0. There is no risk in the G Fund. That is unless you fear our government helping themselves to it, but that isn't the kind of risk we are measuring here. You'll have to look elsewhere to measure that one. I wouldn't know where to start. It makes my head spin clean off. :cheesy:

 

[Cactus]

Please post a link to your source.

For which parts do you mean? I do have some hyperlinks to wikipedia and investopedia for the definition of some terms. I can provide more if you like. Do you mean the source of the data? I got the returns of our Funds from the TSP site www.tsp.gov. If there is something specific, let me know. These are just my ramblings from what I've been able to figure out so far. Feel to comment on it, correct it or set people straight. It's all about teaching folks how to do this for themselves.

Let me know if you want this moved somewhere else. I started this about 2 months ago and originally envisioned it as a blog contribution. This got too big and that didn't seem practical. This looked like an appropriate place to me so I put it here. It also gives others a chance to add their 2 cents worth and teach us some more.

 

[nnuut]

Sorry you are doing fine I just thought you were using something you found on the net! Great work I couldn't even attempt it. Continue please!

 

[Cactus]

Thanks, nnuut.

Let me just add that I realize that most folks here are into charting, but Standard Deviations aren't that mysterious. If you've looked at Bollinger Bands, those are typically just a +/- 2 Standard Deviation Channel around a 20 day SMA. The width of the channel actually shrinks and grows giving you a pictorial representation of how the daily volatility changes over time.

For anyone who hasn't seen this, go to a charting site like StockCharts.com - Simply the Web's Best Financial Charts . Enter $SPX for the S&P 500 index and press go. The Chart that comes up will show the 20 & 50 day SMA by default. Go down to the overlays menu and select Bollinger Bands and press enter. There you go, a pictorial representation of a daily Standard Deviation. This one defaults to 20,2 but you can change it to something like 50,1 and it will draw a 1 Standard Deviation Channel on either side of the 50 day SMA.

 

[Boghie]

Well Cactus, you caught me...
But I am a computer programmer - so I cheat. Quicken's IRR (Internal Rate of Return) is the CAGR. It is a very nice tool to use to get a more real number...

Anyway, the PIP thang on the TSP page is a CAGR/IRR as well..

Your Personal Investment Performance (PIP) for the past 12 months ending 10/31/2013 is 15.52%.
(Your PIP is posted by the 3rd business day of each month.)

The CAGR also attempts to incorporate your contributions into the equation. I think da'Boyz actually use a modified CAGR internally for the reasons you present. They present to us rubes the flat averages and watch a closer reality incorporating risk and contributions. Very nice thread...

 

[Boghie]

And woe be da'Boy that data mines this site using stats like you do.

Whoops, I would never pick a few favorites out of the AT.

Never, absolutely never.

Never...

 

[Boghie]

Crunching that CAGR into a spreadsheet.

While I would never admit to anyone doing such a thing, some are certainly data mining the successful around here. And some would be more interested in a nice risk/reward analysis. Just saying.

And at least one of the some found a different - albeit much harder - CAGR formula. And, that one might be trying Cactus' formula instead. My guess is that at least one individual on the AutoTracker will rebuild his/her spreadsheet for CY2014. Just saying.

Thanks Cactus. Your formula is far more efficient and far more reliable than someones hack...

 

[nnuut]

Everything being influenced by political and financial news must have a thundering effect on the calculations/

 

[Cactus]

Everything being influenced by political and financial news must have a thundering effect on the calculations/

Not as much as you would think unless you are only using recent data such as the 3 year returns in Table 4.

Looking at the Std Dev for equities for 10 years or greater in Tables 3, 4 & 5 they are all pretty much in the same ballpark. You got to include those loss years to make it realistic.

It will be interesting to recompute the Std Dev for the F Fund after including this year's likely loss. That should bump up the value closer to that of Table 5. Notice that it is much less in all the other tables. Those probably are not really realistic as they don't include the occasion loss year.

 

[Boghie]

Everything being influenced by political and financial news must have a thundering effect on the calculations/

NNuut, that is why that certain individual is sitting at -15% from that individual's selected index marker. Not saying anything, but...

Another reason, is that this year was great for those who are not concerned about risk. The individual in question - who would absolutely never data mine the AutoTracker - values analysis that incorporates risk. Said individual hates going -15% one year and +20% the next. But, said individual - who shall remain absolutely anonymous - was a dumb@ss this year and watched the failed lawyers play at politics. And, that damn raven kept cawing 'Never more'.

 

[Boghie]

The early analysis of this thread - before my bloviating - has value...

The CAGR is a good analysis tool. Don't compare the resulting risk based return to an average return that does not reflect the variance in the market. Talking to you Burro. It is an unfair analysis. Compare your returns to the S&P 500 CAGR for a more fair analysis.

By the way, here is the Money Chimp CAGR for the S&P 500

 

[PessOptimist]

Thanks for bumping this thread, I was going to go looking for it. Now I got to find ut how to do the risk/reward thing that is on the board somewhere. I need to change my B&H ways for the next two years but really don't want to sit in G either.

PO

 

[Boghie]

Thanks for bumping this thread, I was going to go looking for it. Now I got to find ut how to do the risk/reward thing that is on the board somewhere. I need to change my B&H ways for the next two years but really don't want to sit in G either.

PO

PO,

Your 2008 - 2015 CAGR/Risk is 6.30% / 5.01%. That is pretty darn good ole boy. Means that you don't lose money. And the CAGR (6.30%) is always less than the average return. But, there is always a butt, you started posting in the AutoTracker in 2009. There was a monster in the house in 2008.

Cactus has a good formula you can use in a spreadsheet. Mine is based on the MoneyChimp formula, but is more manual. Since a CAGR is a metric both are good as long as the use stays consistent...

 

[PessOptimist]

PO,

Your 2008 - 2015 CAGR/Risk is 6.30% / 5.01%. That is pretty darn good ole boy. Means that you don't lose money. And the CAGR (6.30%) is always less than the average return. But, there is always a butt, you started posting in the AutoTracker in 2009. There was a monster in the house in 2008.

Cactus has a good formula you can use in a spreadsheet. Mine is based on the MoneyChimp formula, but is more manual. Since a CAGR is a metric both are good as long as the use stays consistent...

TSP says 2008 PIP was -.23%. CAGR (Cacti's?)spreadsheet I did a while ago based on 12 periods says AAGR 0%, CAGR -.04% and total return -.51% for 2008.

I haven't always been B&H and did move most of TSP to G in late 08. Was slow moving back in 2009 and made several moves in 2009 and early 2010. Then I pretty much stopped messing with it as I was screwing up I thought.

Thanks for the input.

PO